A "random" bunch of numbers, is not so random!
Introduction
Let’s say that you are doing a demographics survey where you ask people about their salaries, monthly expenses, their ages, and a bunch of other demographics. At the end, you write all these numbers in a big giant table. Now ask yourself this question:
How many times do you plan to see the digit “1” in the table?
You are probably thinking, it is plainly 10% of the times, since one of the digits from 0 to 9 will be there, and it is mostly just a bunch of random numbers.
Okay, now ask yourself this question:
How many times is there “1” as the leading significant digit?
Well, it is not so hard. Since 0 cannot be the leading significant digit, so again it is random between 1 to 9. So the answer is 1/9 or about 11.11% of the times.
Unfortunately, this is mostly WRONG!
You will see the digit “1” as the first nonzero digit approximately 30% of the times!
Let’s try again with a different scenario: Let’s consider a bunch of numbers containing the batting scorecard of various cricketers. And to this, let’s add a wildly different dataset about the humidity of Kolkata for the last 2 years.
Now ask yourself the same question: How many times would you see the digit “1” as the first significant digit?
The answer is still the same: It is about 30%.
It looks like the seemingly random bunch of numbers follow some universal law of pattern about their digits. The following is the first statement of this law:
The law of probability of the occurrence of numbers is such that all mantissae of their logarithms are equally likely — Simon Newcomb
A more mathematically precise statement is given by Frank Benford, after whom the law was named “Benford’s Law”.
What it means is that:
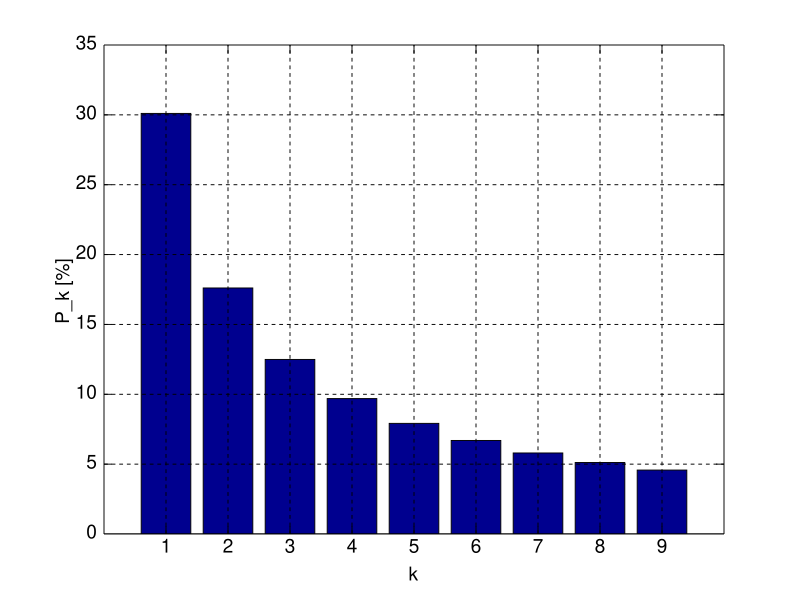
The probability that the first digit is 1 is about 30.1%.
The probability that the first significant digit is 2 is about 17.6%.
…
The probability that the first significant digit is 9 is merely 4.5%.
That is, the probability of the first significant digit decaying logarithmically.
Apparently, the bunch of random numbers does not have randomly distributed digits. In this post, we will explore some more interesting empirical evidence of this law, their applications, and try to understand theoretically why it holds.
More empirical evidence
To convince you further, here’s what I did. I took last year’s share prices for some of the largest stocks, in India and in US, namely:
Reliance, HDFC Bank, Tata Motors, Infosys from Indian stocks.
Apple, Microsoft and Walmart, from US stocks.
After I collected the data from Yahoo Finance, Then, I calculated the percentage return and use the following code snippet to calculate the most significant digit of the return numbers.
And the result of the frequency distribution of the digits was again — as you have guessed — the “Benford’s law”.
A bit of history lessons
Simon Newcomb, in 1881, was performing some experiments to measure the speed of light. During one of these experiments, for some calculations, he needed to look up some logarithmic tables (In 1881, we did not have computers to calculate logarithms so easily). These tables were arranged in an alphabetical way, so the first pages would contain logarithms of numbers that start with 1. Then, we would have the next few pages with logarithms of numbers that start with 2 and so on.
What Newcomb observed is that, the first few pages of the table are more worn out than the rest of the booklet, as if most people are interested in finding logarithms of numbers that begin with 1, compared to finding logs of numbers that begin with 2 or more. So, he just made a mere comment that possibly the digit of seemingly natural physical constants has a pattern.
Later in 1938, physicist Benford found this phenomenon across 20 different datasets. His data set included the surface areas of 335 rivers, the sizes of 3259 US populations, 104 physical constants, 1800 molecular weights, 5000 entries from a mathematical handbook, 308 numbers contained in an issue of Reader's Digest, the street addresses of the first 342 persons listed in American Men of Science and 418 death rates — widely different types of datasets.
After his discovery, many more people start to find examples of this law. Even you can pick up any random statistical table printed on a newspaper and validate this, all you need, is a moderately large bunch of random numbers.
Theoretical Explanation
The most notable theoretical result around Benford’s law is by Theodore P. Hill, and much of my discussion below resolves around the ideas presented in his paper, which is also available online.
There are two major ideas of his proof.
The mixtures of random “bunches”!
The first observation is that Benford’s law do not apply to a single dataset, but a mixture of multiple kinds of data sources. For example, consider the dataset containing the CIBIL score of people. It always ranges between 300 to a maximum of 900, hence there is no way you can have a score with the first significant digit equal to 1 or 2. Hence, Benford’s law does not apply directly.
What it means is that, for Benford’s law to apply precisely, you need datasets of various forms: “Combine the molecular weight tables with baseball statistics and areas of rivers, and then there is a good fit”, but not any individual dataset.
To illustrate this point mathematically, let’s consider how we usually do statistical theories. We start with a sample of observations, distributed according to a fixed probability distribution P.
Usually, we denote it as X₁,X₂,...,Xₙ ∼ P.
But Hill considers a tweak to this system:
You have different probability distributions P₁,P₂,...Pₖ which are some randomly chosen distributions from a collection of all possible probability distribution functions. (For example, P₁ can be normal distribution, P₂ can be uniform distribution, and so on).
For each of these distributions, you pick a sample of “n” observations.
So at the end, you have a bunch of numbers, some from “normal” distribution, some from uniform distribution, some from exponential distribution and so on.
In summary, Benford’s law does not apply to “a bunch” of random numbers, but “random bunches” of numbers! That means, first, you gotta pick some random datasets, and then take a few numbers from each of them!
The scale invariance principle
The second key idea that Hill used (he did not come up with it originally, Donald Knuth mentions this principle around 1965) is the “scale invariance” principle.
The distribution of the “digits”, if universal, should be free of any units of measurement, hence remain the same even if all the numbers are scaled proportionately by any fixed nonzero number.
Let me illustrate this principle with a concrete example: Consider measuring the volume of bottles of different soft drinks (say Coke for example). Most of the standard companies use a metric system, hence you will find bottles of 100ml, 200ml, 500ml or even a litre of coke. There will be some deviations, like instead of a litre of coke you might have 995ml or 1.023 litre, both of which indicate that:
The first digit of these numbers will mostly be 1, 2, 4, 5 and 9.
Therefore, the probability will not decay logarithmically. For example, it is highly unlikely to get a first digit 3 here.
And it is precisely because, the production system (or the data generating mechanism) depends heavily on the units of measurement. For example, if instead of the metric system, we measure the volumes of soft drinks in gallons, the resulting digit distribution will be completely different.
Therefore, we assume a “scale invariance” principle. That means, if the universal law of the distribution is given by a probability distribution P, then
Now, here’s the mathematical result that Hill proved!
A distribution over the digits is “scale invariant” if and only if it is the logarithmically decaying distribution as given by Benford’s law.
Here, I show a very short (not so rigorous) proof (not the argument used by Hill) of this result.
Suppose X has a scale-invariant distribution. Then
Now, let Y = log(X) be a transformed random variable. Then, by a change of variable formula of probability, we get
Therefore,
where we use the property that f(t) = sf(st) and apply it for s = exp(a). This shows that the transformed random variable Y = log(X) has the same probability density at both a and (a+t), i.e., it is uniformly distributed. As a result, the original X is logarithmically distributed as stated in Benford’s law.
Applications and more on Benford’s law
Benford’s law also generalizes to multiple digits. In fact, the probability that the first significant digit is 3, the second significant digit is 1 and the third significant digit is 4, is simply given by:
log(1 + 1/314) = 0.00138 ~ 0.138%
This includes numbers like 0.000314..., 3.14… (think about the pi 🥧) or 314…
A very prominent application of Benford’s law is to detect fraud. For example, in accounting, you have lots of different types of accounts and for each account, there are several transactions. If you simply look for the first significant digits of all these transactions, you should expect a logarithmic distribution of the digits. But if it is not very much so, then there is a very much chance that there has been an accounting fraud. Here is a research paper published by the Indian Audit & Accounts Department, on the very same topic.
Similarly, Benford’s law has also been applied to detect issues in political elections, however, there are arguments for and against it. Here is one research article by Deckert et al. that talks more about this.
Conclusion
On a similar note, I was wondering if Benford’s law can be used to detect any data fraud or data manipulations in academics. So, I took the draft of my PhD thesis (which contains multiple tables with numbers from different types of simulations), and used ChatGPT to extract the numbers from it. And then, create a frequency distribution graph as before:
Here is the result:
Well, the frequency of “1” is much larger, but I am astounded by how well it matches Benford’s law! I am possibly more surprised than you are at this point!
For you, maybe you can also see Benford’s law in action — just look at your bank statements and transactions with so many UPI payments (if you are an avid user of UPI like me), and then get the frequency distribution of the digits.
Thank you very much for being a valued reader! 🙏🏽
Subscribe and follow to get notified when the next post is out!
Until next time.





