How Neural Networks can find hidden patterns of your data?
Introduction
To most, Neural Networks are like a general black box tool that works extremely well for many diverse applications. It magically finds the complex patterns in your data automatically that have the most predictive capabilities.
Mathematicians and computer scientists have poked around this black box for quite some time, and now they have some sort of understanding about how this magic works. This is usually demonstrated through a theorem called the “Universal Approximation Theorem”. The result and its proof are full of mathematical jargon (only nerds like me enjoy this 🤓). Here, I present an alternative and intuitive explanation of the trick behind this magical step. Much of this discussion is the ideas presented in Lecture 20 of the High Dimensional Probability course by Roman Vershynin (it is an excellent open-source course that I recommend if you are interested in high-dimensional statistical inference).
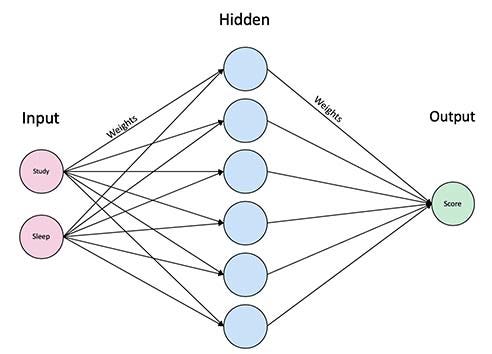
A Quick Refresher on Neural Networks
Before proceeding with the explanation, here’s a brief refresher on neural networks.
Let’s say you have a dataset (x₁,y₁),(x₂,y₂),...,(xₙ,yₙ) , where x₁,x₂,...,xₙ are the predictors or covariates and y₁,y₂,...,yₙ are the response variable that you want to predict. There is an unknown function f such that f(x₁)=y₁,...,f(xₙ)=yₙ. The aim is to learn this unknown function f so that for any new covariate or predictor variable, you can use that function to predict the response.
To give you a concrete example, let’s say you are interested in estimating the price of a house (which is the response y) given the locality, area of the house, number of rooms, number of floors, etc. (all these are covariates, x values). Usually, you will have many covariates as in this example. So, now we denote the covariates as x₁,x₂,...xₚ, (so p-covariates) and the function f becomes
The basis of a neural network is a neuron. A neuron is simply a linear combination of the inputs and then adding a nonlinearity at the end. As shown in the example below, we have the covariates x₁,x₂,...xₚ and some corresponding weights w₁,w₂,...wₚ. The neuron multiplies each x-coordinate with the corresponding weight, and then sums them up, and finally applies some nonlinear function 𝜎 (also called the activation function) at the end.
In mathematical terms, we have
A neural network is usually layers of neurons. Here we consider a simple neural network, where in the first layer, we have a bunch of neurons as above, which produces some intermediate output. Then, in the second layer, these intermediate outputs are combined using a final neuron to predict the response y.
Finally, these weight values (these are often called the parameters of the model) are adjusted so that the final output (from the final neuron) closely approximates the response y, at least for the dataset at hand.
Once you’ve found the right weights, you’ve built the neural network to predict the response variable y.
Thinking in Inner Products
The core of every neural network is the linear combination, between the inputs and the weight parameters. If we consider the input coordinates together as a vector, and similarly the weights as a vector too, then this linear combination can be written as an inner product (also called a dot product).
For now, let’s assume that the first layer is some arbitrary transformation 𝜙(𝐱) of the input vector x. Then, the final response can be expressed as
Let us do one more transformation here, where we rewrite the weights w as a transformation of some other parameter u, i.e., pick 𝐮 = 𝜙⁻¹(𝐰) so that we get 𝐰 = 𝜙(𝐮). (I pray that the God of mathematics forgive for the sin of using 𝜙⁻¹ without ensuring if 𝜙⁻¹ exists or not). Using this new parameter u, we can write
This means that if the neural network were to work, then the inverse activation function applied on the response y should approximately be a dot product in a new vector space, where all vectors are outputs of a transformation 𝜙.
In simpler terms, the above derivation says that the neural networks would work for the housing price prediction problem, only if there exists a transformation of the covariates, such that on the transformed space, the house price can be thought of as an inner product in that abstract space.
Why should such a transformation exist?
Now, the problem of understanding the neural networks boils down to showing that it is possible to build such a transformation 𝜙 that can almost make any nonlinear function as an inner product. Let us try that and see what all sorts of nonlinearities we can build using the form ⟨𝜙(𝐱),𝜙(𝐮)⟩.
Linear Functions
Trivially, we can build functions that are linear in x. For example, if 𝜙(𝐱) = 𝐱, then we have ⟨𝜙(𝐱),𝜙(𝐮)⟩ = ⟨𝐱,𝐮⟩, which is linear in x.
Can we build 5 times ⟨𝐱,𝐮⟩ like this?
Surely we can! just use 𝜙(𝐱)=√5𝐱.
Let’s build exponents
Let’s take this one step further. Can we build squares of those linear functions? For instance, can we build ⟨𝐱,𝐮⟩² as ⟨𝜙(𝐱),𝜙(𝐮)⟩ for some choice of 𝜙?
This is where we need to get a bit creative. Remember that 𝐱=(x₁,x₂,...,xₚ), so we can consider a product of 𝐱 with itself, given by the coordinates
which is simply the coordinates obtained by multiplying each coordinate with each other coordinate in the original 𝐱 vector. And then it follows that
And, if we were to build ⟨𝐱,𝐮⟩³, we can just do the same thing, but this time we will construct the new vectors by taking in 3 coordinates of the original vector x and multiplying them together. In general, for building ⟨𝐱,𝐮⟩ᵏ, we take k-coordinates and multiply them to construct the vector (which can be very huge). The corresponding transformation is often called the k-th order tensor product.
Building polynomials
The next thing is we can build polynomials like this. For example, in order to build ⟨𝐱,𝐮⟩² + ⟨𝐱,𝐮⟩, we can simply consider the transformation of x that first lays the coordinates we need to build ⟨𝐱,𝐮⟩² (i.e., the 2nd order tensor product) and then put the coordinates of the vector x simply. Since the inner product applies coordinatewise, the first part builds ⟨𝐱,𝐮⟩² and the second part builds ⟨𝐱,𝐮⟩ and then the inner product formula sums them up.
In mathematical terms, we get
A fancy term for this representation where we lay the first set of coordinates and then the second set of coordinates is “direct sum”.
Okay, then so far we have been able to build functions like 3⟨𝐱,𝐮⟩³ + 14⟨𝐱,𝐮⟩² + 9⟨𝐱,𝐮⟩, or ⟨𝐱,𝐮⟩¹⁰⁰⁰ + 3⟨𝐱,𝐮⟩³ or anything of that sort.
Building non-linear functions
Now here’s a jump. Using polynomials, we can approximate any continuous function (follows from another approximation theorem by Weierstrass). Therefore, most of the non-linear functions you are familiar with, like sin(x) or log(x) or even sin(log(x)) are all can be approximated by the polynomial functions. And for polynomials, we have already built the transformations 𝜙.
Just to illustrate the point, we can also consider something called a Taylor series. For instance, you’ve probably seen the expansion of the exponential function in this way,
Hence, we can approximate exp(⟨𝐱,𝐮⟩) as ⟨𝜙(𝐱),𝜙(𝐮)⟩ for
I understand that the transformation 𝜙 here is a bit complicated, but it shows that we can create such transformation 𝜙.
This transformation 𝜙 is called a “feature map” and this trick of inner product is called a “kernel trick”.
Optimizing the Kernel
Let us go back to the initial identity we started with, 𝜎⁻¹(y) = ⟨𝜙(𝐱),𝜙(𝐮)⟩. We now know that it is possible to find a transformation 𝜙 such that the above holds. Now remember where we introduced this transformation 𝜙?
It is the first layer of the neural network. Basically, the first layer is now detecting patterns present in this data (i.e., the transformation 𝜙) so that the output can be simply an inner product in this transformed space.
And then, the neural network optimizes the weights in both the first layer and the second layer. The first layer weights, thus, control this transformation 𝜙 and is useful for approximating the non-linear patterns of your data. The weights of the second layer, then find a reference vector u in this newly transformed space.
Often I hear people say that the non-linearity present in the neuron (the activation function) is needed and without that, it won’t work. Unfortunately, the above demonstration should show that it is not entirely true. You can still approximate these non-linear functions. These activation functions help in two ways.
Helps in approximating the non-linearity by using fewer coordinates, hence reducing the number of nodes in the hidden layer.
Helps in approximating non-continuous functions.
Conclusion
While we understand why some simple toy neural networks work in a particular way, we have little insight into the useful neural networks that we use in practical applications. They have multiple layers, and different kinds of neurons (convolutional, recurrent units, gated units, shortcuts, attention, etc.)
Now people might say, my neural network works, so why do I need to learn why it works? Because there’s this saying
Don’t touch a code if it works!
Well, it can save you billions of dollars in training these huge networks. Tensor programs by Greg Wang are an example of that. In case you want to cover them in future posts, let me know in the comments. But be aware that it requires some more serious bit of mathematics than whatever we discussed in this post.
Thank you very much for being a valued reader! 🙏🏽
Subscribe below to get notified when the next post is out. 📢
Until next time.