How statistics saved billions of lives, from the wrath of God
Introduction
A few days ago, one of my friends asked me why I love statistics and decided to pursue a career in it, but not in pure mathematics. When looking back in retrospect, it was possibly due to several factors:
Getting the privilege of studying in a world-renowned institute where the course curriculum was mostly statistics.
Hearing from seniors that data science and statistics are very cool and provide you with a big paycheck.
And math was the only thing I was a bit better at than the average kids of my age in my locality, so my parents thought “This guy loves counting”!
Although all of these motivated me to pursue a career in statistics, there was not much passion involved. I neither loved nor hated statistics like I loved solving puzzles and playing mathematical games (check out the books by Raymond Smullyans). I always used to joke with my mom about my choice:
See maa, statisticians and astrologists both predict the future, so they are like mortal enemies. Since I hate astrologers in general, I need to become a statistician.
But over the course of years, I started to collect impressive stories about how people applying simple statistical tools created applications that changed the world. Over the years, I have grown fond of statistics and started to appreciate it more because of its profound impact on our lives, most of which we are unaware of. I thought, in this post, I would share some such stories here, so statistics saved billions of life, and sometimes altered the course of history.
John Snow’s “The Map of Cholera”
In August of 1854 on Broad Street in London, a newborn infant of the Lewis family, began vomiting and emitting watery, green stools that carried a pungent smell. Sarah Lewis, her mother, while waiting for a local doctor, lost her child in the grip of cholera. Over the next three days, 127 people near the locality of Broad Street became victims of this hazardous disease.
Although cholera was known to ancient Indians from 500 BC (the writings of Charak describe the disease and its prevention in detail), the cause of it was not known to the British Empire till 1831. Even then, it was only known that “Vibrio cholerae”, the bacteria responsible for cholera, was born due to low sanitation conditions and out of human wastes. Among multiple theories about how the transmission of the disease took place, the most popular one was the “miasma” theory or the “foul-smell” theory. Even people thought that it was possible to cure cholera by using “perfumes”: An advertisement in “London Times” read,
FEVER and CHOLERA.—The air of every sick room should be purified by using SAUNDER’S ANTI-MEPHITIC FLUID. This powerful disinfectant destroys foul smells in a moment, and impregnates the air with a refreshing fragrance. —J.T. Saunders, perfumer, 316B, Oxford-street, Regent-circus; and all druggists and perfumers. Price 1s.
But as you possibly guessed, the death parade was not slowing down!
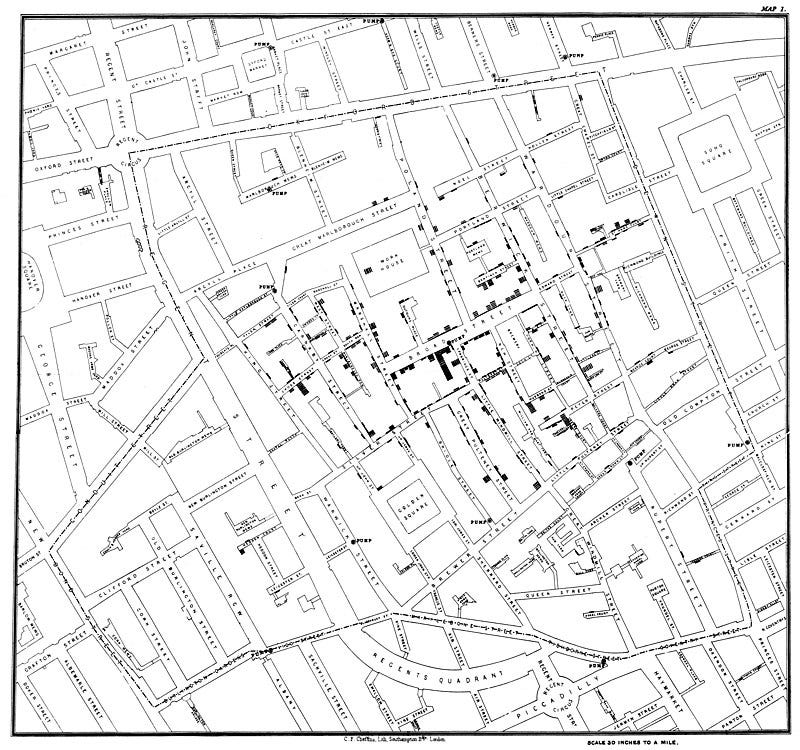
John Snow, a physician of forty-two years old, was not convinced of this miasma theory. He recollected that during his time of apprenticeship, he saw the ravages of cholera firsthand in a local mine in Newcastle — but if it was transmitted by foul air, it would have affected him as well. He came up with a radical yet simple idea: The idea to plot the death victims’ houses on a map. If there are multiple victims in a house, he represented it as a rectangular box much like a bar chart. He called this a “dot map”.
Then he went on to mark different regions on the map based on their nearest water pump. He argued that if the “foul smell theory” was true, then the spread of the disease would have been evenly distributed. However, it was uneven and matched the exact region to a specific water pump at the Broad Street and Cambridge Street crossing.
By providing a simple form of spatial analysis and clustering method, John Snow convinced the local authorities (with the help of churchman Henry Whitehead) to remove the handle and disable the water pump. His work led to further investigations to prove that cholera was transmitted by water, potentially saving hundreds by spotting the epidemic early, at the cost of 616 lives.
More recently, CDC and WHO used similar spatial analysis using dot-maps to identify the ground zero for Covid19 outbreak. John Snow’s work paved a foundation of modern epidemiology using statistical methods.
Reference: The Ghost Map by Steven Johnson
Florence Nightangle’s Polar area diagram
In 1853, the Ottoman Empire (current Turkey) and the Russian Tsar started a disagreement over the rights of the Christian minorities evicted from Palestine. The disagreement grew serious, and Russia invaded the-then Romania. Turkish empire grew restless at this growth of Russia, and they declared war on them. After the Russian Navy destroyed a Turkish squadron in the Black Sea, Great Britain and France joined with Turkey. In September of the following year, the British landed on the Crimean Peninsula and set out, with the French and Turks, to take the Russian naval base at Sevastopol.
This was the pretext that started a 2-year long war called the “Crimean War”.
During this entire period of war, Florence Nightingale was active in her work, taking care of the sick and wounded soldiers. She was so convinced that her work needed to reach at a grander scale, that she began to collect proofs, in the form of data.
After 4 years of data collection, in 1858, she printed a booklet, “Notes on Matters Affecting the Health, Efficiency and Hospital Administration of the British Army”, with the intention of clearly conveying her message of what has gone behind the Crimean War. She came up with a completely original idea of display, by which she can show the causes of death of the soldiers, month by month. But the display had to be very simple and elegant to understand: as if the graph should force the British government to take action to improve healthcare.
Her graph was like a pie chart, but each slice represented a month advancing in the clockwise direction. Each slice is then segregated into 3 parts of different colours, the “blue” area represents the count of soldiers died due to preventable diseases, “red” area shows the count of soldiers died from war wounds, and “black” area is the count of deaths due to “other” causes.
While this graph was that time called popularly at “Polar area diagram”, but later Stigler’s law of eponymy made this called as the “Coxcomb chart”.
Once you see Nightingale's graph, the terrible picture becomes clear as a glass. The Russians were a minor enemy. The real enemies were cholera, typhus, and dysentery.
Her data visualizations and analysis convinced the British government to improve sanitation in military hospitals, leading to a dramatic reduction in deaths due to diseases.
Possibly, in some other country, in some other places, a fierce women like Nightangle needs to eloquently show what the “reality” is, to move the political powers to step in and improve things for good.
Reference: Biographies of Women mathematician
The German Tank Problem
During World War II, the allied forces heard from their intelligence that the Germans were secretly producing a lot more tanks than it seems, and it is just that they are planning on using them all at once for an ambush. This was really a letdown, but there was “almost” no way for them to know how many tanks the Germans were producing.
Wait! I said “almost” … until a statistician came up with an interesting idea.
The analyst (I don’t know if it was a he or she, so I went with a gender-neutral language here) told the army soldiers to note down the serial numbers of the “gearbox” of the captured or destroyed German tanks. It was known that the serial numbers on the “gearbox” was integers like 1, 2, 3… and so on. And at every month, the count restarts from 1.
So the mathematical problem was like this. There are some unknown N number of gearboxes, numbered like 1, 2, 3, … , N. And whenever you capture a tank, you get to see a random serial number from this range. For example, say N = 100 (unknown). In that case, you may see numbers like 34, 73, 49, 44 and 87. So based on these 5 numbers that you see, the goal was to somehow estimate N (i.e., 100).
Let’s work out a simple example to illustrate to you the process that we can use to estimate this: Let’s say we see the numbers 19, 40, 42 and 60.
Can N = 50? - Clearly no, since we already see that there is serial number 60. In fact, N cannot be anything lower than 60.
Can N = 60? - Yes it can be. But it is very unlikely that we have randomly come across the last serial numbered tank itself. Clearly, it seems “intuitively” more likely that N is something larger than 60.
Can N = 100? - Yes it can be, but this is also very less likely, because it means we have not stumbled across any tank with serial numbers from 61 to 100.
So a good estimate of N should be above 60 (the maximum serial value we have observed), but not have too much gap from 60. What is the most likely gap then?
One solution is to take the average gap. That means, we look at the gaps: (40 - 19) = 21, (42 - 40) = 2, and (60 - 42) = 18. The average gap is (21 + 2 + 18)/3 = 13.67 ~ 14.
So, a “good” estimate of N can be (60 + 14) = 74.
In mathematical terms, this means:
Using this kind of simple statistical methods, the Allied analysts were able to estimate the production rate of German tanks, and accordingly modified the production rate of their own tanks.
Without this, the end picture of World War II could have been different.
After the Allied forces were victorious, German records were pulled in and matched against the statistical estimates, which were extremely close to the true records compared to the way-off intelligence estimates.
Source: The Clever way to count tanks - Numberphile.
Another WWII story - Wald’s Bullet Holes
In the year 1943 during WWII, the Allied forces found another problem, and this time it was up in the air. The German’s anti-artillery guns were taking down the American bomber planes, and lots of hits. So the military was thinking of reinforcing the armor of the planes. But reinforcing the entire part of the plane would cause more problems than the solution: It would make the planes heavier, meaning more fuel and less leftover space to carry the bombs.
At this juncture, the military reached out to the Statistics Research Group (SRG) at Columbia University. Abraham Wald, a renowned statistician at that time, was assigned to solving this very problem. The military was kind enough to provide him with data, recording the places of the bullet holes on the bomber planes. We do not have the original data (of course, as the army is involved!), but it looked similar to this:
It was seen that most of the bullet holes were on the wings and the fuselage, where very little was in the place closer to the engines. So the military was under the impression to add armor to the fuselages, where the damage is the most.
A Google search on “Abraham Wald and Bomber planes” will reveal you an amazing story from here on out:
Wald looked at this data and said to the military, No! you need to add armor to the engines instead, where there is no bullet holes. Because, if the bullet hits were distributed randomly, there we should have bullet holes all over the planes. But why the holes near the engines are missing?
Either because the German anti-artillery guns were targeting the fuselage only. Or because the missing bullet holes are on the missing planes, that never came back. — The second one is the more plausiable reason.
However, the real story was not exactly this: To be precise, regarding Wald's work on aircraft damage we have (1) two short and rather vague mentions in Wallis' memoir of work on aircraft vulnerability and (2) the collection of the actual memoranda that Wald wrote on the subject. That's it! Everything else is possibly made up by the commons to make the story look more interesting.
The thing is, often you cannot even advise or suggest the military to do something. The military decisions are taken by the military only. In the case of Abraham Wald, it was no different. Wald did not say no directly, because he was smart enough to know that the army wouldn’t listen. Instead, he made his points obvious in his report — like Florence Nightingale’s polar chart.
In his report, Wald set up to answer the questions:
What is the probability that a plane survives and returns back, given that it has been hit by a bullet in this location?
What is the probability that a plane survives and returns back, given that it has been hit by N bullets? (N = 1, 2, …, 5)
His report was technical. But his assumptions at the beginning were clearly stated. It stated the data collection problem in the light of “survivorship bias”, you have only the data from the planes that have not gone missing or taken down due to enemy fires. So the data you have is of the survivors alone.
After some technical calculations, the probability that a plane survives given it has been hit by a bullet close to the engines, came out to be near zero. He wrote this eloquently in the conclusion of his report.
Resource: The Legend of Abraham Wald
We don’t know how many military planes were actually saved because of Wald’s reports. But we know that he provoked all the statistical researchers to carefully re-examine all the assumptions underpinning the mathematical model, and the data collection. Often, it reveals the limits of what we can or cannot do!
“Survivorship bias” is present everywhere. Most prominent is the presence of influencers — the only ones whose videos will reach out to you are the ones who have survived, and who have made it to be successful. While their success stories inspire us, Wald’s survivorship bias story makes us painfully aware that we are looking only at a very small picture, and the generalization of these stories should be taken with a pinch of salt.
There are plenty more stories like this where simple statistical ideas changed the course of history for a better future.
Feel free to share any interesting story like this you know in the comments section below.
Subscribe below to get notified when the next post is out. 📢
Until next time.






Loved the story on the tank production. It showed the true power of statistics.