Reinforcement Learning (Part 3) - Markov Decision Process

This is the third part of the Reinforcement Learning series: Here I discuss about the representing the reinforcement learning problem as a markov decision process, explain standard terminologies, ...

Introduction

In my previous post (given below), we ended up with a question about how to formally express a reinforcement learning problem, and how should it be represented when the underlying distribution of the system (i.e., the slot machine) itself is changing based on the arm you are choosing. The solution is given by a concept called Markov Decision Process.

This is the third part of the Reinforcement Learning series of blog posts.

Follow StatWizard and subscribe below to get interesting discussions on statistics, mathematics and data science delivered directly to your inbox.

Markov Decision Process (MDP)

Before defining what a Markov Decision Process (MDP) is, let us summarize the process by which reinforcement learning happens, along with the components involved in the process. There are mainly two major components:

• An environment (for the k-arm bandit problem, it is the slot machine), and,

• An agent (the gambler who wants to pull the arm and win rewards).

These two components act in the following way:

1. The environment has a state Sₜ at time t, which is an abstract representation of the environment features that are useful to the problem of learning. For instance, when you are playing chess or any board game, the state is the position of all the chess pieces on the board. When you are playing pinball, the state is the value of all the pixels on the computer screen. When you are driving to the airport and you want to find out which road requires minimal time, the state could be the traffic and weather conditions.

2. Given this state Sₜ (which are the features of the environment as measured by the agent), the agent tries to take one of the possible actions Aₜ at time t, which is an element of the action space 𝒜. Basically, this means that once you see the chess position, you have a set of valid moves that you can play with. For the pinball game, there are only two valid actions at every state: lifting the left flipper or the right flipper. For driving to the airport example, your action is limited to the roads that you can take at every crossing you encounter.

3. Given this action Aₜ acted on the environment, the environment spits out a reward Rₜ₊₁ to the agent and its transforms to a new state Sₜ₊₁. The agent's objective will be to maximize these rewards over time (both over the short and long term, we will get to that shortly). In chess-playing, the reward is +1 when you win, (-1) if you lose the game and 0 for everything else. For the pinball game also we can define a similar reward: the points whenever the ball bounces off an obstacle. For the driving scenario, every mile you drive more is going to cost some fuel which can essentially be thought of as a negative reward.

Now MDP is a decision process as above with an additional Markovian property that the states Sₜ contain all necessary properties of the environment that an agent needs to take an action, the knowledge of the entire history of the states S₀,S₁,...,Sₜ₋₁,Sₜ does not provide any additional benefit.

In terms of probability, these can be written as

\(\begin{align*} P(A_{t+1} \mid S_t) & = P(A_{t+1} \mid S_t, S_{t-1}, S_{t-2}, \dots ),\\\\ P(S_{t+1}, R_{t+1} \mid A_t, S_t) & = P(S_{t+1}, R_{t+1} \mid A_t, S_t, A_{t-1}, S_{t-1}, \dots), \end{align*} \)

The Objective of the RL Agent

The primary goal of a reinforcement learning (RL) agent is to learn a policy that maximizes the reward over time (Surely, this is a capitalistic world!). Now, maximizing rewards over time can have two contrasting viewpoints:

1. The RL agent tries to look for short-term gain and get instant gratification by maximizing its immediate rewards. This is essentially what we would do for the driving example, taking the shortcut road every now and then.

2. The RL agent can also be designed in a way to maximize gains over a very long horizon, essentially delaying gratification by waiting for the right opportunity or building success over time. For instance, a chess grandmaster would do this by thinking 10-20 moves ahead.

To represent both of these paradigms properly, we can use a trick from Finance, namely discounting future values by the inflation rate to obtain a present value. We define Gain at time t as

\(G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots\)

where 𝛾 ∈ [0,1] is a discounting factor. Now, if you want a very long-term view, you can modify 𝛾 to be very close to 1, on the other hand, if you want the RL agent to take a short-term view, you would want 𝛾 to be near zero or zero.

Therefore, instead of focusing on maximizing rewards, the RL agent would aim to maximize the gain Gₜ for every time step t, and would take the action “a” that has the maximum possible gain.

Standard Terminologies

Before diving deeper into the Markov Decision Process, let's clarify some standard terminologies commonly used in reinforcement learning:

• State Space (𝒮 ): The set of all possible states that the environment can be in. States encapsulate all relevant information needed for decision-making.

• Action Space (𝒜 ): The set of all possible actions that the agent can take. The choice of action at a certain state influences the subsequent state and the received reward.

• Policy (𝜋): A policy is a strategy or decision-making function that maps states to actions. It defines the agent's behaviour in the environment. A policy can be deterministic or stochastic. So you can think of 𝜋 as a collection of conditional probability distributions on the action space 𝒜 given the current state s, for all s ∈ 𝒮.

• Transition Dynamics (P ): The probability distribution over the next states and rewards given the current state and action. It characterizes how the environment responds to the agent's actions. Basically, it is the probability distribution over the new state and reward pair (Sₜ₊₁, Rₜ₊₁) conditional on the current state of the environment Sₜ and the RL agent's action Aₜ.

• Value Function (V𝜋): The expected gain starting from a particular state and following a specific policy 𝜋. It represents how good it is for the agent to be in a certain state under the policy 𝜋. It is mathematically described as V𝜋(s) = 𝔼(Gₜ|Sₜ = s) where 𝔼(.) denotes the expectation operator.

• Quality Function or popularly known as Q-Function (Q𝜋): Similar to the value function, but it takes both a state and an action as inputs. It represents the expected cumulative return starting from a certain state, taking a specific action, and then following policy $\pi$. It is mathematically described as Q𝜋(s, a) = 𝔼(Gₜ|Sₜ = s, Aₜ = a).

Making a Better Decision

Now that we are aware of the basic terminologies in the world of Markov Decision Processes, we can formalize the aim of an agent through concrete concepts.

The RL agent wants to maximize its returns in both the short term and the long term, which means to increase its gains over time. However, gain Gₜ is a stochastic quantity, meaning that it can be random due to the random reactions of the environment through its transition dynamics. The straightforward choice is to consider the expected gain 𝔼(Gₜ), and try to maximize that. But 𝔼(Gₜ) has a name, the value function, which is a map from the state space to real numbers. Some states are basically more rewards, hence having more value and other states are less rewarding. The RL agent would always try to take actions that makes it move from a less rewarding state to a more rewarding state, thus increasing its chances to obtain a greater gain.

Let us try to understand this in the context of chess gameplay. You, (say the RL agent), want to win the game. So, one possible strategy you can take is starting from the 50/50-chance at the beginning of the game, for every move that you take you try to increase your winning chances. But, how your opponent plays is not in your control, so it is very difficult to determine your winning chances at some particular chess position (call it P₀). Now think of a situation, where you played 100 average chess players, all games starting from position P₀ and you win 82 of these games. Then it is quite easy for you to say, that particular chess position P₀ has a value of 0.82, as you won 82% of the time. Now imagine you have such data on every possible chess position that can ever occur, then Congratulations! you have cracked a formula for winning every chess game out there, as with every move you take, you can try to create a chess position that is favourable to you. However, it turns out you cannot do this for chess (since the number of possible chess positions can be huge, about 10¹²⁰), so we have some approximations to work with, which I will cover in upcoming posts.

Therefore, one of the fundamental thing for an RL agent to improve its action is to known where it stands, by basically estimating the value function (i.e., the expected gain) for its current policy (read for its current strategy).

Example Game

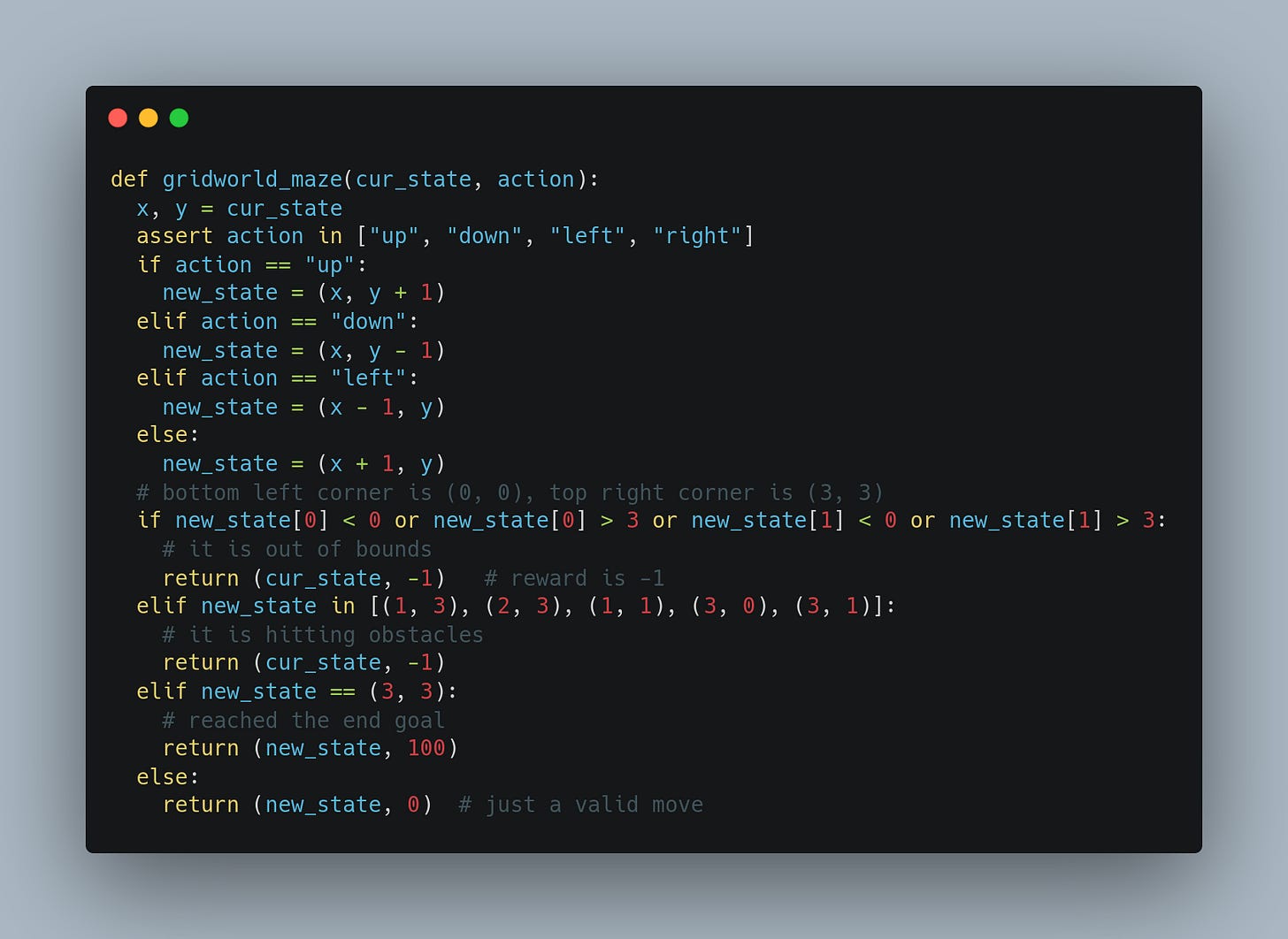
Here, we shall see how an RL agent can try to estimate the value function. For that, we will use the following example game, which is like a maze game within a 4×4 grid. The mission is to start on the top left corner (shown in Red) and reach the top right corner (shown in Blue), but there are some obstacles (shown in Gray) along the way. The state is the agent's current position in the grid, and at any point, it can move up, down, left or right. Every move it makes gives no reward normally, unless it reaches the end when it gets a reward of 5 and hitting any obstacle gives a reward of (-1).

Let us try to code this environment in Python, which takes the current state Sₜ and the action Aₜ, and returns the new state Sₜ₊₁ and the immediate reward Rₜ₊₁.

Now assume that the RL agent behaves randomly. At any state Sₜ, it randomly picks any of the 4 actions, going up or down or left or right. We wish to obtain an estimate of the value function of different states, assuming that the RL agent follows this random policy. Essentially this means to find out which squares in the maze are more important (or closer) to reach the goal when the RL agent is only doing exploration by trying all possible actions.

Monte Carlo - Accumulation of Experiences

Now to obtain an estimate of the value function V𝜋(s), one simple way is to let the agent play a lot of these maze games and see how much rewards it can accumulate from these games, starting from which states, outlined as follows:

1. Say the agent plays the game for 1000 times.

2. At each game, once the game is over, we see a path S₀, R₁, S₁,...,Rₙ, Sₙ. Here, Sₙ is the end goal at the top right corner.

3. Calculate the gains starting from a state along these paths. For example, call G(S₀) = R₁ + 𝛾 R₂ + 𝛾² R₃ +..., G(S₁) = R₂ + 𝛾 R₃ + ..., and so on.

4. If there are repetitions in S₀, S₁,… Sₙ, then the corresponding gain is taken to be the average of all the repeated gains. For example, say S₁₀ is the bottom left corner, and then circling around the obstacles, the agent again comes back to the bottom left corner as S₂₀. Then, the gain for the bottom left corner is taken to be (G(S₁₀) + G(S₂₀)) / 2.

5. Finally, by repeating this process for each game, we have a list of gains for each state coming from different games. We can average these gains out and get an approximate value for each state.

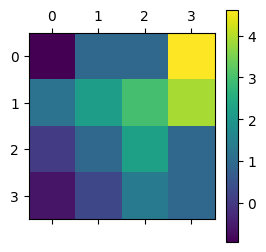
We implement this strategy to get an estimate of the value function in the following code. However, to make it more efficient, instead of keeping a list of gains to average out, we keep a counter and the current value of the average and incrementally update the average after every round/episode / game. The code and the resulting estimates are shown below.

If you see now the heatmap generated from the value estimates, it clearly shows the shortest path the agent needs to take in the maze, just follow along the lighter shades. Hence, just by estimating the value itself, the agent knows how to find a good policy to solve the game.

Bellman Equation - Fixed point iteration

The previous strategy we used required us to simulate the experiences of playing the game itself, and then accumulate those experiences to get a good value estimate. In contrast, if we know the dynamics of the environment completely (i.e., which action triggers which state and rewards), we can theoretically come up with a formula for estimating the value function.

Here's how we do this.

\(\begin{align} v^\pi(s) & = \sum_{a \in \mathcal{A}} \pi(a \mid s) E(G_t \mid S_t = s, A_t = a),\\ & \text{we rewrite the value in terms of policy probabilities and conditional gains for an action}\\ & = \sum_{a \in \mathcal{A}} \pi(a \mid s) \sum_{s' \in \mathcal{S}} p(s' \mid s, a) E(G_t \mid S_t = s, A_t = a, S_{t+1} = s'),\\ & \text{we now do a further conditioning over the next state and introduce the transition dynamics}\\ & = \sum_{a \in \mathcal{A}} \pi(a \mid s) \sum_{s' \in \mathcal{S}} p(s' \mid s, a) E(R_{t+1} + \gamma G_{t+1} \mid S_t = s, A_t = a, S_{t+1} = s')\\ & \text{since, } G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots = R_{t+1} + \gamma G_{t+1}\\ & = \sum_{a \in \mathcal{A}} \pi(a \mid s) \sum_{s' \in \mathcal{S}} p(s' \mid s, a) \left( R_{t+1} + \gamma E(G_{t+1} \mid S_{t+1} = s') \right) \\ & \text{here, we use the markov property}\\ \end{align}\)

Finally, we get the Bellman Equation.

\( v^\pi(s) = \sum_{a \in \mathcal{A}} \pi(a \mid s) \sum_{s' \in \mathcal{S}} p(s' \mid s, a) \left( R_{t+1} + \gamma v^{\pi}(s') \right) \)

Therefore, one way to estimate the value function is to start with some initial estimate of the value function. Then use the right-hand side of the above equation to get a better estimate, and then iterate this process over and over unless we reach a stable estimate of the value function. Note that, you need to have the policy distribution 𝜋(a|s) and the transition dynamics p(s'|s, a) for this strategy to work. Fortunately, we have both of them available since we know the game exactly and know how the environment will respond.

The resulting value estimates turn out to be as follows.

Notice that, the heat plot is very similar to the one for the Monte Carlo estimates, and it also demonstrates the optimal path to solve the maze game. This method is popularly called Value Estimation using Dynamic Programming in Reinforcement Learning literature.

Why value estimates are different?

So we estimated the values using two different methods: accumulating experiences through the Monte Carlo method, and iterative computation of the Bellman equation. Although both shows the same path, the resulting value estimates are slightly different. So, which one is correct?

Turns out the Monte Carlo estimate is correct in this case. The Bellman equation uses on crucial fact that, Gₜ = Rₜ₊₁ + 𝛾 Gₜ₊₁. Now this only holds if there are an infinite number of moves in the game and there is no end of the game, it continues even after the game ends. But in our maze example, the game ends when the agent reaches the top right corner (the blue corner) which makes it a terminal state. Hence, the above relation is only approximately true in this case.

On the other hand, the Monte Carlo method requires a terminating state, otherwise, you cannot perform the accumulation step where you refine the value estimates.

Questions to think about!

Here are some questions to think about before the next post.

1. What kind of games would have no terminal state? Even if it is not a game, try to think of some situation where you can apply RL.

2. Often you don't know how your opponent/environment will behave if it is a two-player or multi-player game. Then, can you combine Monte Carlo with the Bellman equation to create an algorithm that works even for infinite games?

3. How to get an optimal or best policy if there are multiple actions all of which improve the value of the current state? Should we just greedily pick the best one? Or should we explore?