Vision Transformers - Connecting what you see with what you describe!
In this post, I explain the stories behind Image based neural networks, and more specifically the role of Vision Transformers.
Introduction
Recently my friend Srijit created a beautiful walkthrough tutorial on a step-by-step guide on building a Vision transformer architecture in neural networks from scratch (please do check out his GitHub for source code and his substack). From him, I came to know about this paper, I dug around a bit and found some amazing details on why this is such an important step towards achieving the full potential of AI. I am going to share my learnings in this post.
Neural networks, as I have mentioned multiple times in my previous posts, are broadly machines that imitate how a human brain processes information. One of our primary sensory organs is our eyes, hence it is natural to think about neural networks that take images or visual cues as inputs. This is in contrast with how most of us work with AI (e.g. ChatGPT) nowadays, where the communication takes place entirely in texts. The vision transformer, which I will focus on in this post, is in the former group. However, we will circle back to the other group in the later part of this post and explain how, with newer versions of ChatGPT, you can paste in images, alongside textual inputs.
How do you read an image anyway?
Now when I ask how you can allow a machine to read an image, there are actually two subtle questions lurking behind.
For any image, how do you convert it into numbers so that computers can understand it? Well, turns out it is necessary since computers are actually pretty dumb, they only understand zeros and ones.
Let’s say now you input a bunch of numbers representing the image into the computers. Now how you do make sure that the computer sees and interprets the image in the same way that you do? What if, you give it an image of your pet cat “Tom” and it interprets it as an image of a “Porsche 911”.
Let’s start by answering the first question.
Converting images to numbers
Before we talk about how we can convert images to numbers, let us take a moment and think about how we see images through our eyes. Inside our eyes, there is a cornea which is like a lens that takes in light from outside and focuses it onto photoreceptor cells (also called cone cells). There are 3 kinds of cone cells (red, green and blue), and each of them lights up on particular wavelengths of the light. Finally, our brain puts these together and creates a mixed version of these 3 primary colours.

A pixel of an image (i.e., the smallest part of an image) is thus, represented by 3 numbers, between 0 and 1, one for red, one for green and one for blue. These numbers represent what proportion of the particular type of cone cells might light up, 0 representing no cells will light up and 1 representing that all cells will fire up. An image is then a matrix (two-dimensional array) of these pixels. Hence, an image can be inputted to the machine as a 3d tensor, w pixels wide, h pixels high and 3 channels (for red, green and blue). Mathematically, an image I,
where pᵢⱼₖ is the pixel value at i-th row, j-th column and k-th channel.
Numbers to abstract meaning of an image
Let’s now proceed to answer the second question. Once we input these numbers into a neural network, how can we ensure that the network understands the image as we visualize the image naturally?
Consider the image shown below, take a quick look at it for 5-10 seconds!

Now that you’ve taken a look at it, if you want to describe it to someone else, you’ll probably say,
I see some train tracks with trains in it, the timing is a sunset, there are few apartment building on the horizon, and some buildings to the left part. The sky had some scattered clouds.
But if you’re asked whether you can tell what the pixel value of the top left corner of the image is, you probably won’t be able to tell. Therefore, we understand the images as a whole, not pixel by pixel. Also, if you consider a blue pixel on the part of the sky, chances are that the neighbouring pixels are also similarly blue as they are also part of the sky. Therefore, it is not meaningful to look at each individual pixel for the image but to look at an average over blocks (or patches) of the images.
For example, for a 3×3 patch, we can look at an average of the sort
which produces a pixel. Now, as we go over the image, it makes sense to move these 3×3 patches over the entire image, and for every patch take their average. In general, one can consider any q×q patch, and instead of a sample average, take a weighted average. Mathematically, this can be shown as
where wₛₜ are the weights corresponding to the cell at the intersection of s-th row and t-th column of the q×q patch. A beautiful visualization of this is produced by Vincent Dumoulin,
This kind of averaging process is called a Convolution. Usually, in a convolutional neural network (CNN), these types of convolutions are applied layer by layer, and usually at the end, the final layer output is flattened into a long vector. This flattened vector are then considered to be a representation of the image, or its meaning, similar to the word embedding.
If you don’t know what embedding means, do check out my previous posts on Generative AI Series.
The weights in the convolution process are usually kept as parameters, which are chosen using optimization routines like gradient descent during the training step of the neural networks.
I won’t dwell much further on this. A very interesting discussion on this is already available by Grant Sanderson on his channel 3 Blue 1 Brown.
Limitations of a CNN
Imagine when you are reading a science fiction story. At the back of your mind, you start to imagine certain pictures of how a futuristic society would look like. You begin to imagine spaceships and whatnot, and all these are based on visual cues present in immersive texts.
Similarly, let’s say your friend shows you a picture of his pet cat, in the back of your mind, you will associate the word “cat” with the image. And then if you see a cat meme on the internet, you will be able to remember the image you saw earlier, because of the textual connection between the subjects present in the images.
Therefore, the meaning behind an image and the meaning behind the words to describe the image should be able to connect together. In other words, if a machine truly understands an image, it should be able to describe it perfectly. In reverse, the machine should be able to conjure up an image based on your description of it.
Unfortunately, a CNN-type architecture does not work on this principle. It provides the meaning of an image based on a vector (that is derived from multiple iterations of the convolution process), but the end result vector for an image of a cat might be different from the embedding vector of the word “cat”, obtained from a language model.
What it means is that, you can compare “cat images” to “dog images” (🍎 to 🍎), and compare the word “cat” to the word “dog” (🟠 to 🟠), but not “cat images” to the word “cat” (🍎 to 🟠), even though we humans can compare them.
Therefore, we need a common technology that powers both the word embedding and the image embeddings so that they both map to the same space of concepts (or meanings). This space is often called a shared embedding space or a multimodal embedding space.
So, how’s Vision Transformer different?
Achieving the commonality between these different types of models was extremely difficult, at least till 2020. This is because most of the text-based models were built on top of RNN (Recurrent Neural Network) architecture which prioritizes the ordering of the words in a sentence. In contrast, the CNN models, popularly used for visual learning problems, concentrate on modelling spatial dependencies ignoring the ordering of the pixels.
With the advent of transformers based architecture in 2017, scientists realized that it might be the foundational idea that was missing connecting these two different types of models, and finally, in 2020, with the release of Vision transformer, the idea took a concrete shape.
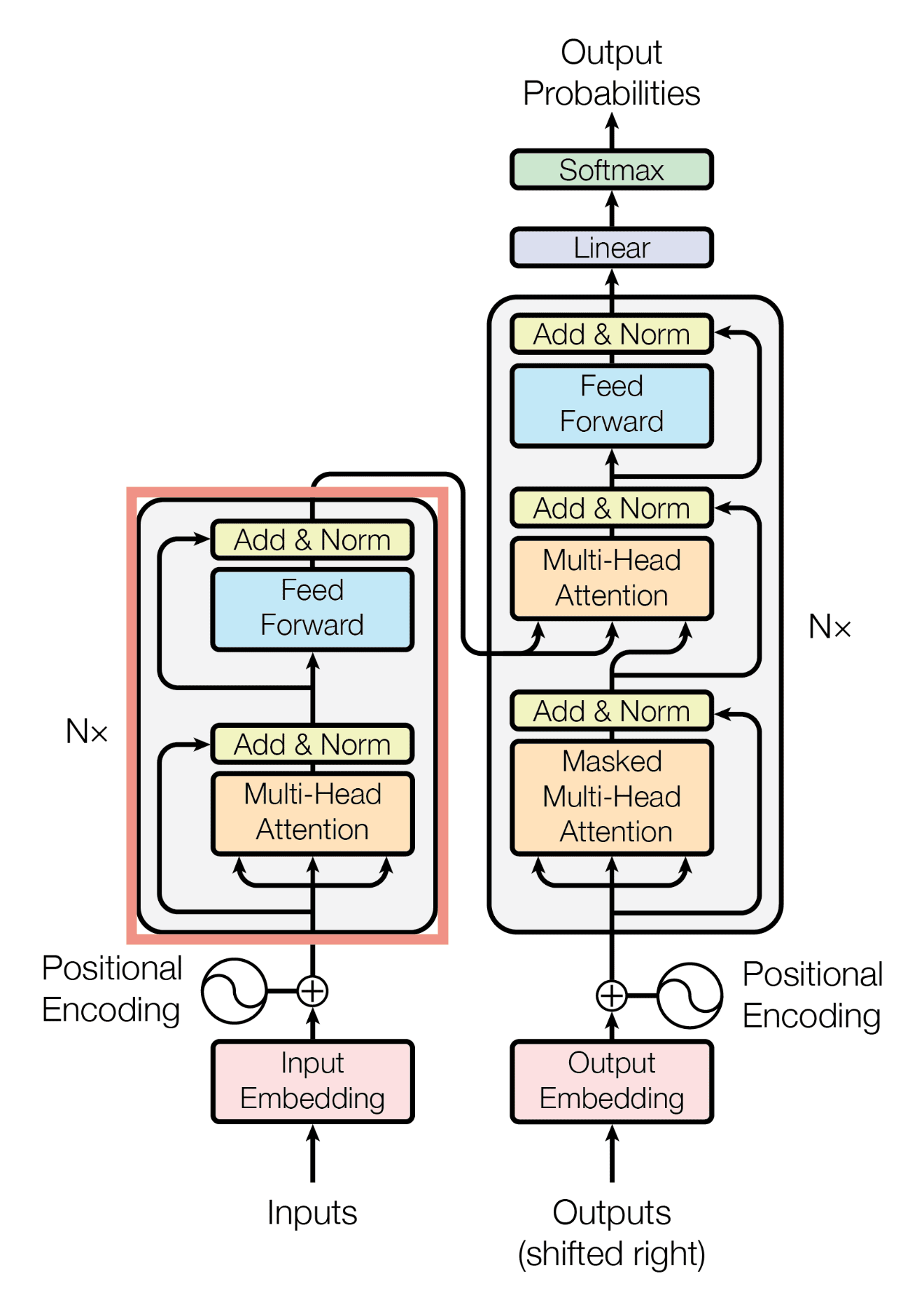
What is a transformer?
At its core, think of a transformer architecture of a neural network as a machine that takes in an input and its surrounding context, and maps them to a vector representing concepts. To understand it better, let us again consider an example. Imagine you don’t know anything about “cats” and want to learn about them. Assume you are in a city where there’s no internet, so the only way to learn about them is to go to a library and read books 📚 on “cats”. Now there will be some books like “Alice in Wonderland” where the Cheshire Cat can speak human language, and there will be some books that will picture a cat as they actually are. To understand them properly, you will probably reach out to the librarian and ask for all the books that have cats in them (probably as tags). Once you read all the books provided by the librarian, your concept of “cat” will be based on a combination of the concept of “cats” described in those books. Probably you will have the understanding that some “cats” can speak and some cannot.
In mathematical terms, you have vectors v₁,v₂,... (called value) representing all books, and their tags are represented by k₁,k₂,... (called keys 🔑). Your query i.e., the word “cat” is represented by a query vector q. Then, the transformer models your concept of “cat” as
i.e., ⟨q,kᵢ⟩ tells you the affinity between the book tags and your query, and then the softmax function converts these affinities into nonnegative weights so that greater affinity yields larger weights and vice-versa. Then, your concept of “cat” will be an accumulation of the corresponding concepts of the books, adjusted by the weights. This particular transformation is called a “single-head attention block”.
The entire transformer is then a collection of these single-head attentions (called multi-head attention) along with a series of standard normalization and feedforward layers.
Transformers for Images
To use the transformer architecture for images, we again take up an analogy. But first, I will show you an animated image below.
Now the question is, can you tell how many dots were shown in the picture?
Chances are, you won’t be able to tell. However, an ape (our ancestors), most likely will be able to. This ability is called Subitising. According to Wikipedia,
Subitising is the ability to look at a small set of objects and instantly know how many there are without counting them
Turns out, apes are usually very good at this because they have to quickly count the number of enemies behind bushes and tree branches in a forest, and based on that count they need to decide on a fight or flight response. From an evolutionary perspective, early humans, instead developed languages to quickly communicate across distances to meet this survival needs, so they did not develop the ability of subitising. Tetsuo Matsuzawa’s talk is a good resource if you want to learn more about this.
However, what this exercise tells us is that we humans don’t see the images as a whole, but rather scan the image from left to right in small patches (or right-to-left for some cultural differences). This is similar to how we read texts. Based on this key idea, the researchers considered segregating the entire image into small k×k patches, and these patches are arranged from left to right. These are treated like words, which are then feeded into a transformer kind of architecture.
As shown above, the entire image (say 640×480 pixels in dimension) may be split into patches of size 16×16, so the entire image ends up being a sequence of length 1200. And now, it should be obvious why the authors of the Vision Transformer model ended up choosing this apt title for their paper,
“An Image is Worth 16x16 Words: ….”
These small 16×16 patches are usually very simple, and contain only one subject, and their meaning can be obtained using an embedding layer and may be based on a one-step or two-step CNN. Once the individual patch-level representations are obtained, they can be feeded into the transformer architecture, which combines the underlying concepts and gives meaning to the whole image.
What do we gain from all that?
Finally, since transformers are the common architecture that powers both textual and visual models, now the meanings that these models output become comparable. Compared to the previous embedding vectors scattered across, we now have images and corresponding words clustered together.
As a result of that, you can now have multi-modal models, i.e., in ChatGPT, you can now upload an image and provide some instructions that uses the concepts present in an image.
For example, here’s an application that I tried with Claude. I have a flowchart diagram image, and I want to reproduce the mermaid code to reproduce the code. If you are not familiar with mermaid, think of this: You find a nice plot in some slides or some paper, and you want to get the code to reproduce the same plot yourself. Or if you are familiar with LaTeX, it is similar to what MathPix does for converting images or snippets of equations into LaTeX code.
Here’s the snippet of the chat between Claude and me.
And the Vision transformer is the first breakthrough that made this possible!
Thank you very much for being a valued reader! 🙏🏽 Feel free to share and comment to let me know about what scientific breakthroughs you feel changed the world!
Subscribe below to get notified when the next post is out. 📢
Until next time.