When you should marry and settle down - according to math!

Nov 07, 2024

Well, who am I to say when you want to settle down 😏, but if you are into dating, and possibly thinking if this is the right person you wanna spend the rest of your live with, then there's a mathematical way to be assured, at least probabilistically. And this is what I am going to explain today in this post.

The setting for dating

Since it rhymes so must be true… what I am going to say next. Imagine that you know that in your lifetime you are going to date a maximum of N persons. However, in reality, you don't know this N. But you can make a reasonable guess on this. For instance, assume that

After meeting with a person, you will probably have 2 dates before rejecting,
You go for the dates on weekends, and you do not go out both days of the weekend (probably too tiring!, and yes, you have chores to do as well!)
You are not dating more than one person at a time.

Well, you can date at most 2 persons during an entire month. If you start dating from 18 and go till 40 years old, basically a 22-year span then you can have at most 524 (=22x12x2) persons to date in your lifetime. So, this can be a reasonable maximum value of N.

In reality, this could be much lower for most people, usually at ranges between 10 to 50. This number N, clearly, depends on how socially outgoing you are to a great extent. Let’s assume you “know thyself” and you have your number N. Now, you try the following:

You date a maximum of N persons one by one, no two at the same time.
Given your current date, you can compare the person with your previous dates and possibly rank them, as per your preference.
If you reject someone, they are rejected for good. You cannot determine later after dating a few more persons that this old date was the perfect prince or princess for you. Well, mathematicians are sadists - so you can not go back to your exes just like in those romantic movies! 😣 Ugh!

And finally, your goal is of course to settle down with the best person among all the dates - that you have had so far, and among the future dates you are going to meet later in life.

The exploration-exploitation dilemma

So, how do we do this? Let us try some simple strategies first.

What if you meet with someone, fall in love at first sight, and think, that's it. That is the soul mate you are supposed to have. But, you do not know what the future has in store for you. So, it is very much possible that this person may not be the best date you could have gotten among all future dates you are yet to meet. This is the problem with picking too fast. In mathematical terms, this is an “exploitation” strategy.

What if instead, you wait for too long, until Prince Charming or Princess Delight comes your way? But then possibly you have gotten too old. So, there is a good chance that you have probably missed your opportunity to settle down with the right person, and have already rejected him/her. For mathematicians, this is an “exploration” strategy.

Essentially you would want something that balances between these two approaches.

Optimal Strategy

Let’s consider what an optimal strategy would look like.

In any such strategy, you will possibly date a few persons, explore your likings & preferences (We call this the exploration period). Then you will pick the next best person. This is because if you don't pick the best person you have seen so far, then you obviously know that the person you are planning to settle down with is not the best choice. Probably this means you can never be at ease. So imagine you "sample" first K persons and then choose the next best person. Let's try to calculate the probability of success of this strategy.

If the best person is in the first "K explored persons" then the algorithm does not let you choose anyone since there is no best person after the "exploration period".
On the other hand, if the first stage does not contain the best person, then the algorithm works only if there is no better person after the first K explored persons and before the position of the best person.
- Assume that the position of the best person is at the i-th position.
- Then the strategy works if the second best person among the first i persons is in the first K dates.
- Equivalently, the strategy works if the best person among the first (i-1) persons is in the first K dates. (Since we already know that the best person appears at position i)

Therefore, the probability is:

\(p_k = \sum_{i=1}^n P(\text{best at position i}) \times P(\text{second best between 1 to K})\)

Since the order in which the dates come is random, we have the first term equal to 1/N. For the second term, it is simply K/(i-1). Hence,

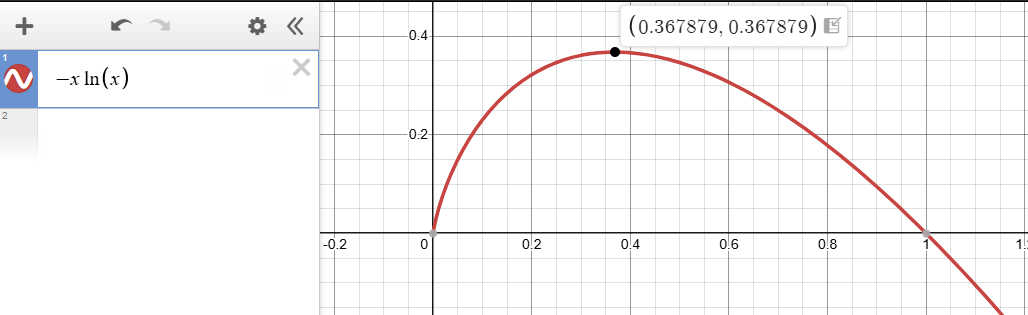
\(p_k = \dfrac{1}{N}\sum_{i=K+1}^N \dfrac{K}{i-1} = \dfrac{K}{N} \times \left( \dfrac{1}{K} + \dfrac{1}{K+1} + \dots + \dfrac{1}{N-1} \right)\)

Now, to figure out this harmonic sum, we can use a bit of calculus to approximate this when N is large. Note that we can rewrite the above as

\(p_k = \dfrac{K}{N} \times \dfrac{1}{N} \times \left( \dfrac{1}{K/N} + \dfrac{1}{(K+1)/N} + \dots + \dfrac{1}{(N-1)/N} \right) \approx x \int_x^1 \dfrac{dt}{t} = -x\ln(x)\)

When x = K/N, i.e., the ratio of the persons you reject during the initial exploration period.

Since your goal is to find the best strategy, it is equivalent to finding the best choice of x, that maximizes the above probability. Again, we can use a bit of calculus, take the derivative of the function (-x ln(x)) and set it up equal to 0, which yields that the maximum is attained at x = 1/e ≈ 0.3678. And, the optimal probability is again 1/e ~ 37%, which is far better than randomly picking someone with probability 1/N for any N > 2.

This means, the optimal mathematical strategy for the above “dating problem” is as follows:

Step I: Reject 37% of the initial dates.
Step II: Then pick the next best date who is better compared to everyone you have dated so far.

This is known as the “37% Rule” in pop culture.

If you want to know more about this, it is just a Google search away. Some notable sources are:

The poem of 37% rule by Earnest Davis.
Martin Gardner’s “New Mathematical Diversions” in 1966, where it probably appeared first in a popularized text.
How To Marry The Right Girl: A Mathematical Solution - National Public Radio.
When to stop dating and settle down, according to math - Washington Post.

and of course, the thousands of other articles and blog posts explaining the same thing that I have described so far. You can go to Google and type “the Secretary problem”.

And with another assumption that your dating age range is between 18 to 40, the 37% rule tells us that you should explore dating till you are 26, and then marry the next best person 🤵👰 you meet with.

All the math nerds out there, I presume so far you have had a great time sharing these articles with your friends and telling them really the mathematical way to live life. (There are a few more interesting things like this in the book “Algorithms to Live By”, which can inspire you!)

But all the common folks (specifically non-mathematicians) out there, you guys are probably thinking…

This sounds fishy!

Yes, it is indeed. There are a few underlying assumptions under this whole story which is not often highlighted. This is often the case: whenever a scientific result is popularized by not-so-scientist people (most reporters and common masses, just for the sake of getting more readers), it ends up being distorted or applied to a completely different setting where the assumptions may not hold true.

For example, this problem was originally described as the “Secretary problem”, where you are interviewing people for a single position of a secretary, and in this case, most assumptions are met. But they don’t necessarily translate to the situation when you are searching for potential suitors. Some details of this misapplication are presented in this article by Ernest Davis and this amazing TED Talk by Hanah Fry.

A society where everyone follows math!

Suppose, there is a society where everyone follows this mathematical rule to find their suitors. Therefore, every individual in this society:

Rejects first 37% of suitors just to perform exploration. That means, from 18 to 40 years old, they reject all dates before turning 26.

That also means, nobody in this society marries before the age of 26.

They settle with the best date with a probability of 37% i.e., the probability that the algorithm succeeds.

That means, approximately (100 - 37)% = 63% people in the society do not find any partner to marry at all, and stay single.

Clearly, as you can see, sticking to the “algorithms of life” can be pretty harsh!

You have a preference for your dates, and so has the person sitting opposite of you!

For courtship specifically, there is another serious problem. The dates that you have are not just sitting there waiting to be chosen, they have their own preferences as well. Even if you are playing this game of choosing the best person, you might just fall during their “exploration period”, which means you will be rejected, and you must keep moving forward to look for the next best person.

Math also has a solution for this setup. Assume that whenever you pick a person, with some probability q, the person may be unavailable.

To solve such a system, we need a few more ideas:

Let, the state of the system be (k, r), where k is the number of persons seen so far, and r is the number of persons you have dated between the best person so far and your current date.
Let, V(k, r) be the probability of a strategy that starts out at state (k, r). We want to figure out V(k, 0).

Then, as shown in this paper, one can get a dynamic programming equation

\(V(k,r) = \max\left[ \dfrac{k}{N}(1-q) + V(k,\infty)q, \dfrac{1}{k+1}V(k+1, 0) + \dfrac{k}{k+1}V(k+1,r+1) \right]\)

To understand this consider the following:

Starting out in state (k, r), if you find the best person (in the entire sequence) they could be available with probability (1-q). If this person is not available, then the algorithm provides no match for you.
On the other hand, starting out in state (k, r), you can have an apparent best person with probability 1/(k+1). If that is the case, then r becomes 0, so you have the term V(k+1, 0). If you get anyone else, then the apparent best person does not change, and your state becomes (k+1, r+1).

Now, one can either use Monte Carlo simulation (to common folks, think of it as some sort of computer programming) or some theoretical calculations on recurrence relations to figure out the solution.

And the solution,

…drumroll please…

\((1-q)^{1/q}\)

which for the case with q = 0, becomes same as 1/e ~ 37%. With q = 50%, the probability of the strategy reduces to 25%, as shown in the figure below.

Should you always go for the best date?

Here’s an excerpt from the article by Ernest Davies,

I tell a tale to illustrate the problems with the algorithm. Strephon lives in Arcadia with 100 eligible bachelorettes. He’s happy to date them all, so N = 100. Therefore, following the algorithm, his plan is first to date 37 of them, and then to marry the next one who is better than any of those 37.
However, the course of following algorithms never did run smooth. Date 17 is Chloe, who is amazing. Strephon is completely smitten. However, a theorem is a theorem, and Strephon can easily calculate that the probability is .83 that someone he hasn’t met yet is even better than Chloe. Goodbye Chloe.

At the end of the tale, Strephon never finds someone. He met a few more amazing people on his future dates, but none of them liked him. But Chloe liked him, so it would be much better for him to settle down with the second-best or third-best choice, instead of going for the best choice.

There are two ways you can convert this to mathematical reasoning.

You have prefixed a value R. You are fine with finding a match with any of the top-R persons. (e.g., R = 3 means you are okay with matching with any of the top 3 persons you will date in your lifetime). This time, again you can set up a recurrence relation as before to find out the “exploration period”. As you would have expected, if you are okay with increasing R, the “exploration period” can be much shorter. This infographic from TED explains it all:

If you’d be happy with anyone in the top 15 percent, you only need to spend 19 percent of your dating life finding what’s out there. Use this strategy and you can expect a whopping 78 percent chance of success — much less risky than the traditional all-or-nothing version of this problem.

The other way to solve this mathematically is to maximize the “expected match”. In this case, you do not prefix any R, but instead, you score each person you have dated so far in the inverse of their rank. That means, if you have dated 10 people so far, the best person gets a perfect score of 10, the second-best gets a 9, and so on. The computation in this case is a bit more involved, but this post by Maxwell Jones explains the derivation.

The result??

Turns out the exploration period in this case is (√N − 1) many dates. That means, for a dating age range of 18 to 40 years, the optimal exploration is about 21 years and 8 months.

Everything depends on N, and you!

Well, so far, we assumed that we know N, the total number of dates you will have in your lifetime. Clearly, you don’t know this.

There are some mathematical solutions where you consider this N to be random, distributed according to some random variables (e.g. Uniform, Poisson, Geometric). For uniform distribution, the “exploration proportion” becomes about 27%, while for Poisson and Geometric, usually there is no change in the 37% rule. It kinda shows you how universal the rule is, even if we don’t know N.

However, the major problem here is you. Suppose you consider yourself an introvert and think that for you, N is probably 10. So you go over 10 dates over two decades, and then, looks like none of them gets your vibes properly.

Should you just stop dating now, as the 10 dates are over? Because the algorithm would be inconsistent otherwise?
Should you live your entire life staying single?

These are decisions yours to make, and no algorithm should be telling you what to do.

Final Words!

Problems like this one are mathematically stimulating and fun to solve. But if you try to apply them to a real-world which is messy and complex, you may end up with ridiculous answers like this one, even if things are logically correct.

Assumptions that underpin these mathematical logics are crucial ingredients that are often not iterated enough in the news articles or blog posts presenting them. As a result, the facts are misapplied and conveyed inaccurately. So next time someone shares a post like “You are bored probably means you are a genius and here’s a mathematical proof for that” or “Sleeping 10 hours daily can help you focus more”, …. and similar eye-catching news articles, please read this with a “statistical mind”, because

“mathematical minds” can be pretty easily distorted,

but in “statistics”, the real-life data speaks for itself.

If you know of any popularized articles where scientific facts are distorted, please share them in the comments.