Reinforcement Learning (Part 7) - Solving Lunar Landing

This is the 7th and final part of the Reinforcement Learning Series: Here I give a brief introduction to deep Q-learning and some techniques to increase RL agent's efficiency

Introduction

Hey everyone! In my last post about Reinforcement Learning, we learned about techniques to deal with state spaces of infinite sizes, using the method of linear value approximation. We also solved the Mountain Car problem, and it turned out that adding a bit of nonlinearity like kernel-based features helped a lot to train a better RL agent.

Remember that we learned about the interesting Lunar Lander environment before, where we were trying to train an agent to successfully land a moon rover on the surface of the moon. Here's a picture to refresh your memory.

The goal of this is to train an agent to land on the surface of the moon successfully. It observes state values as an 8-dimensional vector, constituting its linear positions, linear velocities, angular velocities and many more. It simply has 4 actions to do as follows:

1. Do nothing.

2. Fire the left engine.

3. Fire the main engine.

4. Fire the right engine.

Before, we tried to train an agent to solve this with the Q-learning technique, but that did not get us very far. We used sparse encoding to represent the 8-dimensional observation vector to a tabular grid. However, since we now know about the techniques to handle infinite state space, we might be able to do better.

This is the final part of the Reinforcement Learning series of blog posts.

Follow StatWizard and subscribe below to get interesting discussions on statistics, mathematics and data science delivered directly to your inbox.

Kernel Transform and Linear Approximation

We first try the technique with different kernel transformations and their linear combinations, as in the previous post. We consider 400 different kernel-based feature transformations of those $8$ variables that the state vector spits out, and then we try to have a weight vector associated with each of these actions. We take the inner product of the respective weight vector with these kernel features, and that becomes our Q-value for that particular action.

We solved the Mountain Car problem with this technique, in about 200 episodes. Since this is a bit difficult problem compared to that, we allow the agent to train for about 2000 episodes. Well, turns out it learned something useful, but still not decent enough. Here's a picture of the agent after 2000 episodes (It takes about 20-25 minutes to completely run on a Google Colab notebook).

We also tracked the rewards over these episodes. If we look at the plot of the history of these rewards, it looks like this.

Turns out it is not learning after about 1000 episodes, and it is not getting better. Looks like we need something more powerful.

More Power: Let's Replicate the Brain

Well, if we look at the kernel-transformed features from before, it was serving two purposes:

• It was adding some nonlinearities to capture more complex functional forms.

• Having 400 different kernel-transformed features is like having 400 different transformations of the features to work with and that gave us lots of power.

Mathematically, if we have the state vector s = (x₁,x₂,…,x₈), then the action value we were deriving as

\(q(a_i) = w_{1,1}\phi_{1,1}(x_1) + \dots + w_{100,1}\phi_{100,1}(x_1) + w_{1,2}\phi_{1,2}(x_2) + \dots \)

So, what if instead of directly combining these transformed values into features, we try to combine these transformed values into another set of transformed values, and then maybe another set of transformed values, and then another, and so on (you get the idea!) until you are satisfied, and then these whole bunch of these variables can come together to form the final opinion about the Q-value. Mathematically it will be like this.

\(\begin{align*} h_{1} & = \phi_1(w_{1,1} x_{1} + w_{1,2}x_{2} + \dots + w_{1,8}x_{8}) \\ h_{2} & = \phi_1(w_{2,1} x_{1} + w_{2,2}x_{2} + \dots + w_{2,8}x_{8}) \\ \dots & \dots \\ h_{64} & = \phi_1(w_{64,1} x_{1} + w_{64,2}x_{2} + \dots + w_{64,8}x_{8}) \\ \end{align*}\)

and then,

\(\begin{align*} g_{1} & = \phi_2(v_{1,1} h_{1} + v_{1,2}h_{2} + \dots + v_{1,64}h_{64}) \\ g_{2} & = \phi_2(v_{2,1} h_{1} + v_{2,2}h_{2} + \dots + v_{2,64}h_{64}) \\ \dots & \dots \\ g_{64} & = \phi_2(v_{64,1} h_{1} + v_{64,2}h_{2} + \dots + v_{64,64}h_{64})\\ \end{align*} \)

and so on, and finally,

\(\begin{align*} q_{1} & = u_{1,1} g_{1} + u_{1,2}g_{2} + \dots + u_{1,64}g_{64}\\ \dots & \dots \\ q_{4} & = u_{4,1} g_{1} + u_{64,2}g_{2} + \dots + u_{8,64}g_{64}\\ \end{align*} \)

where all these w, v and us are weight parameters which will be changed as the agent learns more and more about the environment. The final output will be the Q-values of all the 4 actions. The functions 𝜙₁ and 𝜙₂ are adding nonlinearities like the kernel. If you draw out the input-output pairs of the above equations as connections, then it will look like as follows, a fully connected Network. (This gives you one part of the story, why Neural Network is a Network).

Another way to think about this network is analogous to the human brain. The human brain is comprised of multiple layers of neurons, each neuron is like a connection you see above. Basically, it takes some inputs and performs a chemical reaction (read it as a linear combination) and the reaction either activates the neuron and sends input to the next layer, or the reaction may die down. McCulloch and Pitts were the first to introduce this idea of representing neural activity by mathematical terms in 1943, and then Frank Rosenblatt implemented the same in 1958, and he named it Perceptron, a machine that does the perception. This should now explain the other half of the name, why Neural Network is Neural.

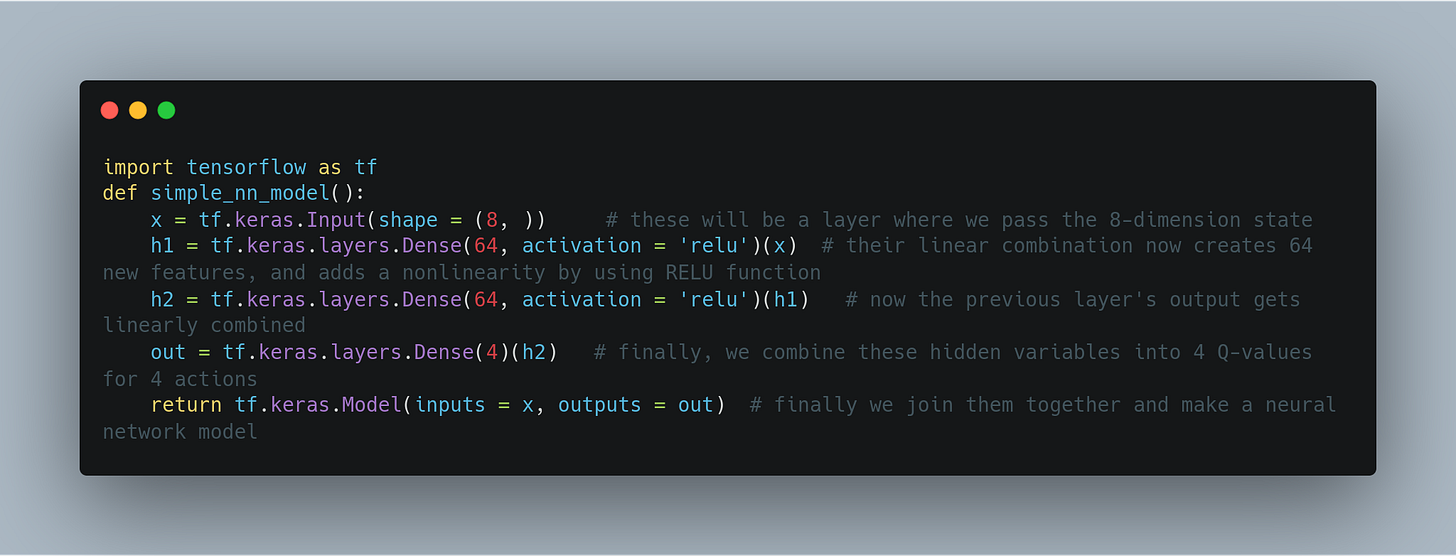
Implementing the Neural Network

Here, we will be using the tensorflow package (developed by Google) to implement this network of neurons.

While our network is pretty simple, sometimes it can be very complicated. Tensorflow models have a nice `summary` function that we can use to extract relevant information from a model.

model = simple_nn_model()
model.summary()


## Output
Model: "model"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_1 (InputLayer)        [(None, 8)]               0         
 dense_1 (Dense)             (None, 64)                576       
 dense_2 (Dense)             (None, 64)                4160      
 dense_3 (Dense)             (None, 4)                 260       
=================================================================
Total params: 4996 (19.52 KB)
Trainable params: 4996 (19.52 KB)
Non-trainable params: 0 (0.00 Byte)

The weights of the above network are randomly initialized, usually from a standard normal distribution. Let's now see how we can use this network to obtain the Q-values for an arbitrary state from the Lunar Lander environment.

state = env.observation_space.sample()   # we sample one observation
x = model(tf.convert_to_tensor([state]))  # run the model on it,
print(x)

## Output
tf.Tensor([[-0.6147699 -0.8249271  5.23029    0.7746165]], shape=(1, 4), dtype=float32)

One particular thing to notice here is that we are passing [state] as as array to the model instead of simply state variable. This is because the neural networks provided in TensorFlow are usually designed to work on a batch of inputs, instead of a single input, so it expects the first dimension of any variable to always represent the batch. Here, making a list out of state variable ensures we pass a 2-dimensional tensor to the model with a batch dimension of 1.

Next, in order to train the RL agent, we need to perform gradient descent to minimize the squared loss between the current value and the target value (which is either TD target, Q-learning target or SARSA target). For linear value approximation, computing the gradient was easy. However, in case of a neural network, you need a bit more use of the Chain rule of derivatives to calculate the gradient. Fortunately, we don't have to do that manually, tensorflow is nice enough to provide an automatic gradient calculator, called tf.GradientTape(). It is a Python execution context that tracks down all operations done within the context and then provides a gradient value through the use of the function tf.GradientTape().gradient().

dense_6/kernel:0, shape: (8, 64)
dense_6/bias:0, shape: (64,)
dense_7/kernel:0, shape: (64, 64)
dense_7/bias:0, shape: (64,)
dense_8/kernel:0, shape: (64, 4)
dense_8/bias:0, shape: (4,)

Now we need to modify the weights of the neural network and reduce them by the learning rate times the appropriate gradient. To do that, we can set up an optimizer in tensorflow, and apply a single step of the optimizer, instead of directly modifying the model variable and its weights.

optimizer = tf.keras.optimizers.SGD(learning_rate=1e-3) # Instantiate an optimizer
# Run one step of gradient descent by updating the value of the variables to minimize the loss.
optimizer.apply_gradients(zip(grad, model.trainable_weights))

Putting it all together

So far, we know how to create a neural network model and how to update the model parameters to reduce the loss function. Therefore, training the RL agent simply requires us to specify the target in each step of each episode, and then take one step towards making the model better by applying the gradient descent rule. Here's how the entire code would have looked like:

We train for 200 episodes first to see what's happening. It takes about 10 minutes in the same Google Colab notebook.

Well, turns out it is always taking the action of doing nothing. The history of rewards tells us that the rewards obtained in the episodes are wildly varying, but on average, it has learned almost nothing.

We had our hopes up with this better model, but let's try to investigate what's causing this issue.

Neural Network: The Data Hungry Monster

There are basically two things that went wrong while training the neural network-based RL agent.

1. Turns out since a neural network is a bit complicated compared to the linear value approximation, hence it requires much more amount of data to effectively train its parameters.

2. In linear value approximation, we could selectively update weights associated with the Q-value estimation for a specific action, hence all the weights were not being updated.

   1. We can have separately 4 different neural networks, one for each action. Then we can selectively update a single neural network for that single action. However, we would want some hidden layer features to be common across all these networks (some features which are important for knowing may be whether to fire some engine or not, and are shared between multiple actions). This is not possible if we use multiple neural networks.

   2. Another problem with this approach is that it does not scale. For instance, if you have 100 possible actions, you would need 100 different networks.

Experience Replay

Experience Replay is one way to address the first concern. Basically, it tells to store some state, action, and reward tuples in a buffer, and when the model needs to update its parameter, it can consume a batch of these tuples from the buffer and train on it. The buffer has a fixed size. When it overflows the buffer, we simply remove the oldest entries from the buffer to keep its size in check.

This method is called Experience Replay because it allows the RL agent to replay some of its stored experiences and keep learning from them over and over. This means, that even when the agent is not interacting with the actual environment, it can still keep learning from its past experiences. Here is how we can implement an experience replay buffer using Python classes. We need two methods in this class. One for adding a new transition to the buffer. Another is to get a batch of transactions for the RL agent to train on.

Batch Update and Double Q-learning

To solve the second concern, instead of having one neural network for each action, we will consider only two copies of the same neural network. One of them will be evaluating the Q-values by keeping its weights fixed for multiple iterations, and another will be updating the weights to find the optimal policy.

Mathematically, it is like having two sets of weights w₁ and w₂. Let us denote the neural network by Q, so 𝛥w₁ = 𝛼 ∇(Rₜ+𝛾Q(w₂;Sₜ₊₁)−Q(w₁;Sₜ))² where 𝛼 and 𝛾 are the learning rate and discount factor respectively. Here, we keep updating the weights w₁ without updating the weights w₂ for several steps. After a fixed number of steps, we finally update w₂ by the current value of the weights w₁. This means the target Rₜ+𝛾Q(w₂;Sₜ₊₁) remains static for several steps, creating a more stable target for the neural network to achieve. This diminishes the chance of having wildly varying reward functions as the number of episodes progresses. This Q(w₂;.) is often called as the evaluation network.

We first make a function that produces the TensorFlow neural network model. In addition to that, we also specify a custom loss function that takes the true Q-values (i.e., as obtained by the TD-target) and the predicted Q-values produced by the current neural network, and produces the squared difference of their maximums. This is exactly what you would get as an error for the Q-learning method.

The last two lines is a bit new, they are preparing the network network model to reduce that loss function. This compilation step has no outside impact, but the model training (i.e., the gradient descent) becomes much more efficient and faster to do.

Now we get an evaluation model, which is a copy of the current neural network, we can use the following function, which creates a blank model using the above function and then copies the weights from the current model to the blank model.

def copy_model(model, LR):
  model2 = simple_nn_model_with_regularizer(LR)   # used only for evaluation, so LR does not matter
  model2.set_weights(model.get_weights())
  return model2

One particular thing you might be thinking is why we did not simply do the simple model2 = model. The reason is that in such a case, model2 simply refers to a pointer to the original variable model that holds the neural network, it does not create an independent copy. Hence, if we perform gradient descent on the first neural network model, the weights of model2 also will keep changing, but we do not want that.

Moment of Truth

So, we combine all of these ideas and put them together in action. Before that, we provide another function that uses the evaluation network and a batch of state transitions from the replay buffer to compute the target values for that batch.

And here we specify the hyperparameters, initialize a bunch of stuffs like our policy and evaluation networks, and also the replay buffer.

It took about 25 minutes to complete the training, although I did a little cheating! Used a free GPU at Google Colab as it was available. Here's how the result looks after 2000 episodes.

Great! Now our lunar lander is successfully prepared to land on the surface of the moon, and this means, you have now added a bit more of rocket science to your awesome store of knowledge.

Conclusion

Starting from an almost zero knowledge of Reinforcement Learning, we have come a long way. Congratulations on making it this far! Hope you have liked the series of posts.

This was a beginner-friendly introductory series for all the RL enthusiasts out there. We tried to learn the basic concepts and implement a few hands-on examples, and we have built a whooping Lunar Lander! If you wish for more posts like this, on advanced Reinforcement Learning techniques, let me know in the comments!

---

Thank you very much for being a valued reader! 🙏🏽

Subscribe below to get notified when the next post is out. 📢

Until next time.