In the last post (if you’ve missed it, find it here), we saw how we can understand the topics behind a bunch of posts about New Year’s Resolutions from X, and then we also looked at some of the problems that come up with Latent Semantic Analysis (LSA) and Latent Dirichlet Allocation (LDA). If I were to recollect (as it’s been a while since the last post), a major issue was:
LSA or LDA treats every word as separate objects, and as a result, it does not know if the words “Hi” and “Hello” mean the same thing.
This is a big problem. A fundamental requirement for performing natural language processing is to understand the relationship between the meaning of different words, otherwise, it is just the same as “categorical data analysis”.
What defines the meaning of a word?
Before we start to undertake the mission of finding the meaning of words, let us first understand how do we know “hi” and “hello” are synonymous words?
Is that because of how it is defined in the Oxford dictionary? I’m pretty sure most of us never bothered to check the meaning of “hi” and “hello” from the Oxford dictionary and verify if they are synonymous, we kind of know because of their usages. This is the key idea: USAGE.
Two words have same meaning because they can be used almost interchangeably. In a large corpus of texts, they are expected to share the same neighbouring words!
For example, “hi” and “hello” have same meaning because they can be used like:
Hi, nice to meet you!
Hello, nice to meet you!
Based on this concept, Tomas Mikolov and his co-authors from Google came up with two new neural network architectures in this paper, namely the CBOW and Skip-gram models, and started a whole new era of natural language processing techniques that resolves around finding meanings of word as numerical vectors.
Understanding embeddings
Before we dive deeper into how these work, let us first understand what we want from this exercise:
Because we want to do statistical analysis, we want to represent each word using numbers.
A word can have different meanings based on the context, for example, the word “bank” may mean the financial bank or the bank of a river depending on the context. So, a single number is too small to represent the complete meaning of a word, so may be we need a bunch of numbers to represent each word. Let us use vectors to represent each word then. (See a similar idea in the post about LSA) We call such a vector as the embedding vector.
The vectors should be something so that the words having similar meanings will have vectors close to each other. The words having different meanings should have vectors away from each other.
For example, if you have three words, “Hi”, “Hello” and “Cricket”, then
Usually, these embedding vectors are normalized to unit vectors. Hence,
i.e., the distance can be written as linearly related to the cosine similarity (or the dot product) between two vectors but with a negative coefficient. Hence, the closer two embedding vectors are, the higher is the cosine similarity between them and vice-versa.
Often, you would expect the vectors to be distributed in a way that represents analogies appearing in natural language in the form of linear relationships.
For example, if you take the vector of “king” and subtract the vector of “male” and add the vector of “female”, you will get something close to the vector of “queen”.
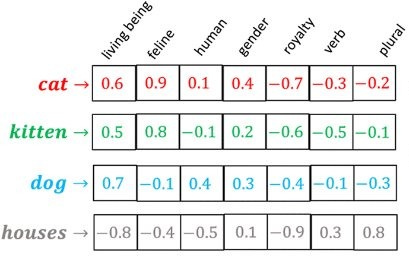
At this point, you might be wondering what these numbers represent. Honestly speaking, nobody knows. But we can sometimes take a sneak peek on these numbers, do some sort of additional processing (e.g. clustering) to make sense out of it. And here’s how you can think about it.
Suppose, you obtain embedding vectors for a bunch of words and write these vectors out in a table as shown above. Then you can see some patterns: like may be the first coordinate is positive whenever the word is a living being, and it is negative whenever the word mentioned is not a living being. As a result, you may think that the first component may represent whether the concept related to the word refers to a living being or not.
And in the same way, all these other coordinates refer to some kind of concept. If the word matches against the concept, the corresponding entry of the embedding vector will be highly positive, and if the word is the opposite of that concept, the corresponding entry will be highly negative.
Therefore, when you hear words like “embedding dimension is 1024” or “embedding vector of size 1024”, in the back of your mind, you should think that each word is being represented by its relationship to 1024 different abstract concepts — the exact list of concepts will vary from one embedding model to another.
Creating embeddings
Now, let’s take our discussion back to the paper on Word2Vec, the technology that helps us create these embedding vectors.
Let us consider a slightly more meaningful example than “Hi” and “Hello”. Namely, consider the sentence:
All that glitters is not gold.
We want to find out the embedding vector for the word “glitters”. As we discussed before, the word “glitters” should be represented by its neighbours, so we consider the words (“All”, “that”, “is” and “not”) as a combined representation for “glitters”. Now there are two ways to proceed.
Suppose you are given a blank in the place of the word “glitters”. Given the neighbours (All, that, is, not), if these neighbours define the meaning of the word “glitters”, we should be able to predict that it is go for the blank. Therefore, we should generate the vector representations such that it helps me predict the vector of “glitters” based on a combination of the vectors of “All”, “that”, “is” and “not”.
On the other way, if we are given the word “glitters” and are asked to come up with a sentence for it, we will possibly come up with the above sentence. Therefore, the vector representation of the word “glitters” should somehow contain enough information to predict the vector of these neighbours.
The first architecture is CBOW (Continuous Bag of Words) and the second one is the Skip-gram model.
Here’s a picture from the original paper that kind of summarizes it.
Let’s talk about CBOW first. Assume that you have 10,000 words in your vocabulary, and for each word, you want to represent them using 256-dimensional vectors. So, in total, there are 2,560,000 (~2M) unknown parameters. Now the CBOW model simply predicts the output word as the word which is the nearest to the “bag” of neighbouring word vectors, using a simple logistic regression-like idea.
Notice that, the closer the embedding vectors of input words and output words are, the greater is their cosine similarity, and the greater the above probability. What CBOW does is that, it takes all the surrounding input words, takes their average vector, and assuming that as the input, uses the above model to calculate the probability of the actual word.
For our example sentence, it would be:
Take the vectors of “All”, “that”, “is” and “not”.
Take their average, i.e., v* = (v(All) + v(that) + v(is) + v(not)) / 4.
Calculate the cosine similarity between v(glitters) and v*, and then exponentiate and normalize to get the probability.
The following is a naive implementation of the same in Python.
Once you have the probability, now you can do the same for each and every word of the entire set of corpus that you have. And then, you can take the log of these probabilities and sum them up, which we “statisticians” call as the log-likelihood. You may think of likelihood as the probability of observing these data provided you have the embedding vectors correctly guessed.
For the case of Skip-gram, you can calculate the log-likelihood by considering two sums, one for summing up all the possible outputs of neighbouring words, and another for summing up over the entire corpus. If you’re mathematically inclined to know, here’s how it looks:
i.e., we try to predict the (t+j)-th word based on the t-th word.
Thus, you can find an estimate of all these embedding vectors, by maximizing these probabilities (specifically the likelihood). Techniques like gradient descent are usually performed to get this. In the original paper, they train it on the “Google News” dataset for approximately 100 million words.
And once you’ve done all that, you can get a numerical representation of every word that way we wanted. If you want to train it yourself, Google provides a very nice and optimized shell script here. Also, here’s a very beautiful 3D visualization from the TensorFlow team that shows the final product of embeddings; see for yourself to get a feel.
Word2Vec Variations
There are two major problems with the initial Word2Vec.
Word2Vec only considers local similarities, i.e., a local context window to describe the word. On the other hand, matrix factorization methods (e.g. LSA, LDA) consider each word based on the information from all the documents combined. So the question is: Are we losing something by focusing on local contexts only?
A more serious issue is that the embedding vectors may not be available for unknown words or mistyped words. For example, instead of typing “cricket”, if someone types “circket”, we understand that both will mean the same thing based on the context, however, the CBOW or Skip-gram model will find no instance of this word “circket” in the corpus, and hence it produces a completely random vector as its embedding. It may not be close to the vector of “cricket”, as we wanted.
The first question was answered by a group of computer scientists from Stanford University in the 2014 paper introducing “GloVe” (Global Vector Representations) while the second question was answered 3 years later in the 2016 paper by another group of researchers from Facebook, by implementing something called “subword embedding”.
GloVe
GloVe proceeds with a similar idea of noting the contextual frequencies of different words. In particular, it considers the simple idea of ratios to calculate the conditional probability of co-occurrence,
Now, consider two words “ice” and “steam”, on which we will do the conditioning. And then we will look at the conditional probabilities of different words. Here’s a table of these probabilities.
For a word like “solid” which is more related to “ice” rather than “stream”, the probability P(solid | ice) will be much more than P(solid | steam).
For a word like “gas”, which is more related to “steam”, the probability P(gas | ice) will be much smaller than P(gas | ice).
For a word that’s equally related to both or related to neither of them, the probabilities should be similar and the ratio should be close to 1.
Therefore, the example shows that rather than trying to model these probabilities like Word2Vec, one should consider the ratio of these probabilities as the starting point, which gives a clearer picture of the meaning of each word. So, we want to have some functional relationship as
Which says that the cosine similarity between the difference between the embedding vectors between conditioning word i and word j, and the embedding vector of the word k should be directly related to the co-occurrence ratio. It turns out, if you carefully write it down and do some algebra, you obtain an objective function of the form
where Xᵢⱼ is the number of times word j appears in the neighbouring position of word i and f(.) is some cost function, and bᵢ, bⱼ are biases. Now, you can again apply standard techniques like gradient descent to minimize the above, and obtain the vector representations of each word.
It is quite clear that GloVe takes localized context information. To understand how it takes “global” information, here’s a simple exercise for you! Take f(.) as the constant function equal to 1, and then you will see that minimizing the above objective function is the same as extracting the first eigenvector for the log-transformed co-occurrence matrix (i.e., cross-product of DT matrix).
Subword Embeddings
The problem that subword embeddings solve is a procedure to handle mistyped words, and out-of-vocabulary (OOV) rare words. Consider the word “glitters” from before. Suppose I consider the mistyped word “gliters” instead (which is missing one l). One way to understand that they are similar is by noting how many characters they share in order (i.e., they share 7 characters, g, l, i, t, e, r, s), or we can look at the pairs of characters (i.e., they share character pairs like gl, li, it, …) and also triplets of characters and so on… you get the idea.
So, instead of trying to capture the embedding vector from the smallest meaningful representation of words, one can consider a “subword” (which is simply a fixed-length sequence of characters) having some representative vectors, and that they get combined together to create the embedding for any word. In other words, for the word “glitters”, we consider the subwords as:
<gl, gli, lit, itt, tte, ter, ers, rs>
The special characters < and > are used to mark the beginning and ending of a word. Now, by decomposing each word into these subwords, one can learn the embedding vectors of these subwords by using the above techniques like Word2Vec or GloVe. And finally, the embedding vector of “glitters” is given by:
i.e., the average of the corresponding subword embeddings. Now, the mistyped word “gliters” will share 6 out of these 8 subwords, hence its vector representation will be somewhat close to the actual word “glitters”. And Facebook AI Research group published the FastText library underlying the same principle of subword-based embeddings, which contains the pre-trained word embedding vectors for 157 different languages now.
Conclusion
Before we wrap up, pause for a moment and think about how can we represent a document using embedding vectors, instead of each individual word. Turns out, yes, and that’s the fundamental idea before we dive into neural network-based natural language processing.
One simple technique (like “Bag of Words”) is to assume the embedding vector of a document to be the average of the embedding vectors of the words it contains. However, this is not a very good idea.
In fact, we need to learn what we can do to ensure that the sentences:
The child hugged the bear. — Cute and Adorable!
The bear hugged the child. — Very concerning!
have different embedding vectors despite having the same set of words in different order, and the two sentences:
What is your age?
How old are you?
have the same/close embedding vectors despite having no common words.
We will see in more detail how this seemingly magical thing happens in our next post.
Thank you very much for being a valued reader! 🙏🏽 If you found this helpful, consider sharing it with a friend or on Twitter/LinkedIn by clicking the share link below. And if you’re new here, subscribe to get notified when the next post of this series is out!
Until next time.